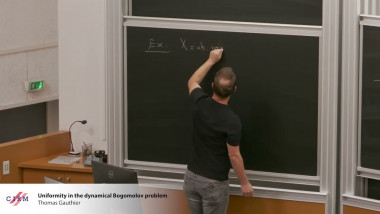By Ray Perlner
Permutation equivalence of codes is a widely studied problem in cryptanalysis. Since 2000 it has been known that random instances of this problem can be efficiently solved by Sendrier's Support Splitting Algorithm. However, support splitting is known to be inefficient when applied to codes with a large hull. This class of apparently hard instances has been utilized, for example, in the recently proposed LESS signature scheme. This talk presents research in progress (joint with Daniel Apon, Maxime Bros, Pierre Ciadoux and Becky Powell) exploring a different approach to solving the code permutation equivalence problem. This new approach uses insights from pure mathematics and cryptanalysis of the lattice isomorphism problem -- in particular the concept of lattice genus. Our preliminary experimental data suggests that the new approach can also solve random instances of code permutation equivalence efficiently, and while there are some difficulties that arise when applying it to codes with large hulls (such as those needed to break the LESS signature scheme) these difficulties may be less severe (or at least different) than those encountered by earlier approaches. More work is needed to determine what can be accomplished with our new approach.
By Ray Perlner
By Edoardo Persichetti
By Joachim Rosenthal
By Mélissa Rossi
By Thomas Prest
By Javier Verbel
By David Jao
By Alexander May
By Luís Brandão
By Chris Peikert
By Thibauld Feneuil
By Federico Pintore
By Jean-François Biasse
By Thibaut Delcroix
By Thibaut Delcroix
By Lorena López-Hernanz
