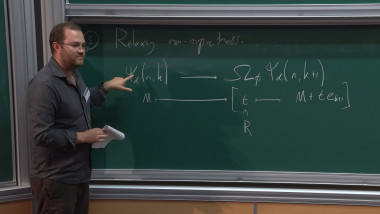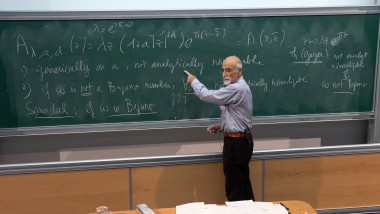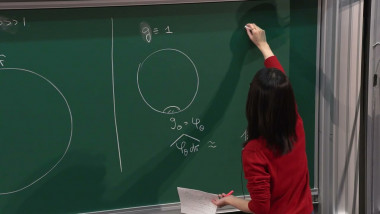Variants of Lojasiewicz's Gradient Inequality
The celebrated Lojasiewicz gradient inequality (L) has an important consequence; the length of a gradient trajectory, between two levels, is uniformly bounded. So, a trajectory has a limit when approaching a critical level. It has inspired Ren ́e Thom to formulate the conjecture that the trajectory has a tangent at the limit. I will describe various versions and extensions of inequality (L). I will state a variant of this inequality, which is valid for a map with values in a finite-dimensional vector space. It yields the boundedness of the volume of a submanifold transverse to the kernels of differentials of the map. This is an analogue of the boundedness of the length of gradient trajectories.