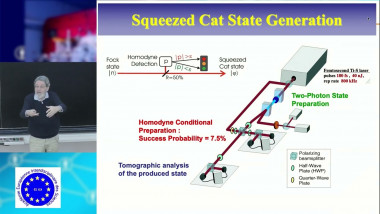
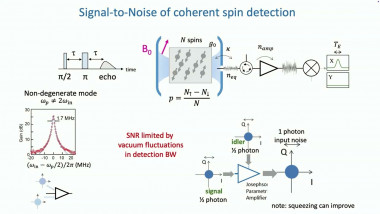
Apparaît dans la collection : 2017 - T3 - WS3 - Quantum information theory

I will present multivariate trace inequalities that extend the Golden-Thompson and Araki-Lieb-Thirring inequalities as well as some logarithmic trace inequalities to arbitrarily many matrices. From our four matrix extension of the Golden–Thompson inequality, I will then deduce various remainder terms for the monotonicity of the quantum relative entropy and strong sub-additivity of the von Neumann entropy in terms of recoverability. The proofs rely on complex interpolation theory as well as asymptotic spectral pinching, providing a transparent approach to treat generic multivariate trace inequalities. Based on [Multivariate Trace Inequalities (with Sutter and Tomamichel)], [Quantum Markov Chains and Logarithmic Trace Inequalities (with Sutter and Tomamichel)], and [On Composite Quantum Hypothesis Testing (with Brandao and Hirche)].