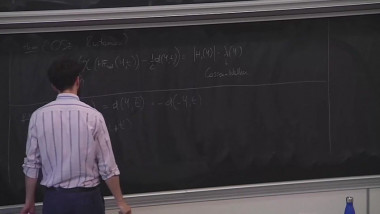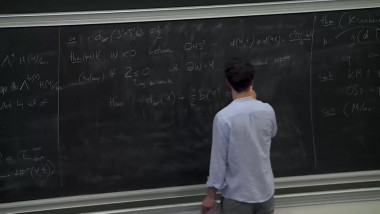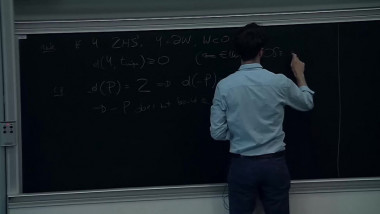Jet bundles and reparametrization group actions occupy a central role in hyperbolicity questions due to the strategy developed by Demailly, Siu, et al., to study the degeneracy of entire curves in projective varieties. We explain how this strategy ultimately reduces the problem to the intersection theory of non-reductive geometric invariant theory-type quotients, which has led to the recent proof of the Green-Griffiths-Lang and Kobayashi hyperbolicity conjectures for generic projective hypersurfaces with effective degree bounds.