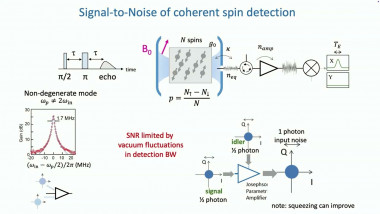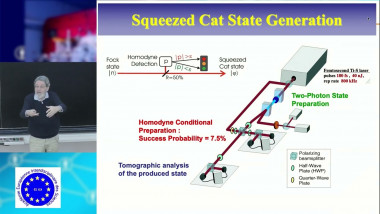
Communications sécurisées avec des variables quantiques continues
De Philippe Grangier

Nonlinear Landau levels (NLLs) in the almost-bosonic anyon gas
De Douglas Lundholm

Łukasiewicz Logic and Tsallis Entropy Connected with Free Projections in the Free and Conditionally Free Probability
De Marek Bożejko
Quantum Error Mitigation Driven by Classical Simulations and Evolution Equations
De Oleg Kaikov