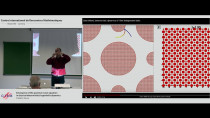
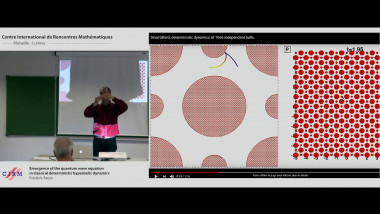
Emergence of the quantum wave equation in classical deterministic hyperbolic dynamics
In the 80's, D. Ruelle, D. Bowen and others have introduced probabilistic and spectral methods in order to study deterministic chaos (”Ruelle resonances”). For a geodesic flow on a strictly negative curvature Riemannian manifold, following this approach and use of microlocal analysis, one obtains that long time fluctuations of classical probabilities are described by an effective quantum wave equation. This may be surprising because there is no added quantization procedure. We will discuss consequences for the zeros of dynamical zeta functions. This shows that the problematic of classical chaos and quantum chaos are closely related. Joint work with Masato Tsujii.