Carmin.tv

Mathématiques
et Interactions

Merci de nous donner votre avis pour que nous puissions améliorer votre expérience !
CEMRACS 2025: Quantum Computing / CEMRACS 2025: Calcul quantique
15 videos

CEMRACS 2025: Quantum Computing / CEMRACS 2025: Calcul quantique

Complex Geometry, Complex Analysis and Dynamics / Géométrie Complexe, Analyse et Dynamique Complexe
5 videos

Complex Geometry, Complex Analysis and Dynamics / Géométrie Complexe, Analyse et Dynamique Complexe

2025 IHES Summer School – Discrete Subgroups of Lie Groups : Dynamics, Actions, Rigidity
36 videos

2025 IHES Summer School – Discrete Subgroups of Lie Groups : Dynamics, Actions, Rigidity

Prime numbers and arithmetic randomness / Nombres premiers et aléa arithmétique
5 videos

Prime numbers and arithmetic randomness / Nombres premiers et aléa arithmétique

Toutes les collections
CIMPA
CIRM
IHES
IHP
Institut Fourier
LMR
SMF
Tous les instituts
Logarithmic and non-archimedean methods in Singularity Theory - Thematic Month Week 1 / Méthodes logarithmiques et non-archimédiennes en théorie des singularités - Mois thématique semaine 1

Collection Logarithmic and non-archimedean methods in Singularity Theory - Thematic Month Week 1 / Méthodes logarithmiques et non-archimédiennes en théorie des singularités - Mois thématique semaine 1

Organisateur(s) Fantini, Lorenzo ; Pełka, Tomasz ; Pichon, Anne ; Rond, Guillaume
Date(s) 27/01/2025 - 31/01/2025
URL associée https://conferences.cirm-math.fr/3267.html
00:00:00 / 00:00:00
20 20

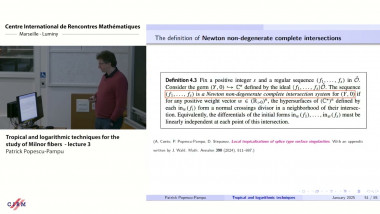
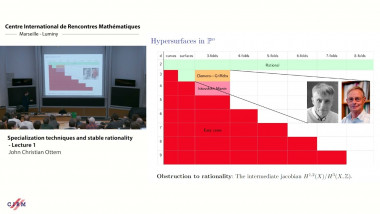
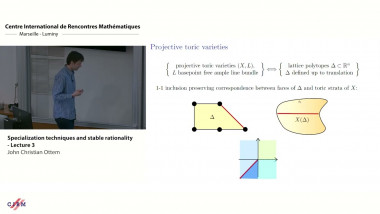
Semi-homogeneous bundles, Fourier-Mukai transforms, and tropicalization

De Martin Ulirsch

Let $\mathrm{X}$ be a fixed abelian variety. In this talk I will outline a framework to classify semi-homogeneous vector bundles on $\mathrm{X}$ using a suitably modified Fourier–Mukai transform that generalizes the well-known homogeneous situation. This will allow us to explicitly construct moduli spaces of semi-homogeneous vector bundles on $\mathrm{X}$. Using the perspective of non-Archimedean uniformization, we can use our insights to understand the tropicalization of the moduli space of semihomogeneous vector bundles in terms of its essential skeleton.This talk is based on joint work with Andreas Gross, Inder Kaur, and Annette Werner.

Informations sur la vidéo

Données de citation

  • DOI 10.24350/CIRM.V.20294903
  • Citer cette vidéo Ulirsch, Martin (28/01/2025). Semi-homogeneous bundles, Fourier-Mukai transforms, and tropicalization. CIRM. Audiovisual resource. DOI: 10.24350/CIRM.V.20294903
  • URL https://dx.doi.org/10.24350/CIRM.V.20294903

Domaine(s)

Document(s)

Dernières questions liées sur MathOverflow

Pour poser une question, votre compte Carmin.tv doit être connecté à mathoverflow

Poser une question sur MathOverflow




Inscrivez-vous

  • Mettez des vidéos en favori
  • Ajoutez des vidéos à regarder plus tard &
    conservez votre historique de consultation
  • Commentez avec la communauté
    scientifique
  • Recevez des notifications de mise à jour
    de vos sujets favoris
Copyright Carmin.tv 2025
En poursuivant votre navigation sur ce site, vous acceptez l'utilisation de cookies pour améliorer votre expérience. En savoir plus sur notre politique de confidentialité.
Accepter
Donner son avis