
A $\lambda$-adic family of Funke-Millson cycles and a $\lambda$-adic Funke-Millson lift
De Paul Kiefer

Modularity of special cycles in orthogonal and unitary Shimura varieties
De Salim Tayou

Cohomology of arithmetic groups and number theory: geometric, asymptotic and computational aspects 1
De Philippe Elbaz-Vincent

Cohomology of arithmetic groups and number theory: geometric, asymptotic and computational aspects 3
De Philippe Elbaz-Vincent
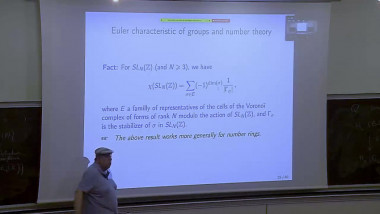
Cohomology of arithmetic groups and number theory: geometric, asymptotic and computational aspects 2
De Philippe Elbaz-Vincent











