Apparaît dans la collection : 2023 - T1A - WS1 - Quantum gravity and random geometry

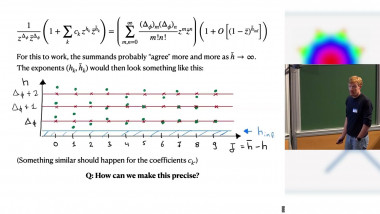
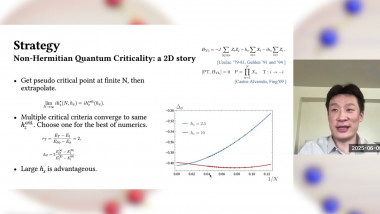
It is challenging to realize emergence of macroscopic spacetimes in tensor models. We study a wave function of a tensor model in the canonical formalism in a certain large-N limit, in which the wave function can reliably be computed classically (namely, by saddle points). We show that spacetimes develop through successive first-order phase transitions, in which numbers of “points” increase one by one. When a positive cosmological constant is turned on, Lie-group symmetric macroscopic spacetimes with locality have large amplitudes.