Le transport optimal en pratique : géométrie, algorithmes et applications
De Jean Feydy
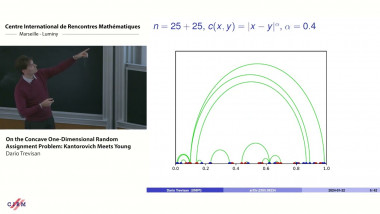
On the concave one-dimensional random assignment problem: Kantorovich meets young
De Dario Trevisan

Relationship between classification and regression in statistical fairness
De Solenne Gaucher

Merging rate of opinions via optimal transport on random measures
De Marta Catalano