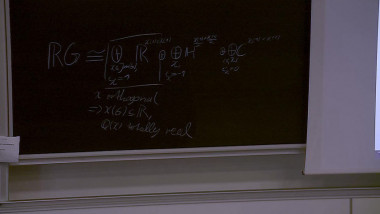De Tobias Moede
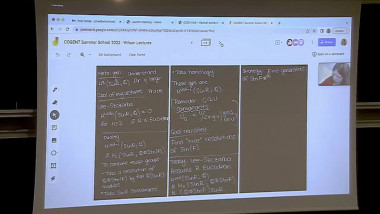
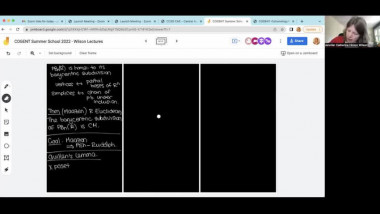
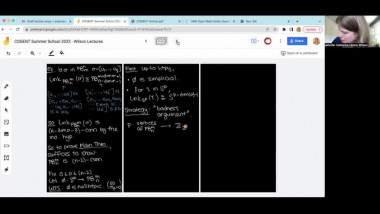
The coclass of a finite pp-group of order pnpn and class cc is defined as n−cn−c. Using coclass as the primary invariant in the investigation of finite pp-groups turned out to be a very fruitful approach. Together with Bettina Eick, we have developed a coclass theory for nilpotent associative algebras over fields. A central tool are the coclass graphs associated with the algebras of a fixed coclass. The graphs for coclass zero are well understood. We give a full description for coclass one and explore graphs for higher coclasses. We prove several structural results for coclass graphs, which yield results in the flavor of the coclass theorems for finite pp-groups. The most striking observation in our experimental data is that for finite fields all of these graphs seem to exhibit a periodic pattern. A similar periodicity in the graphs for finite pp-groups has been proved independently by du Sautoy using the theory of zeta functions and by Eick & Leedham-Green using cohomological methods. We give an outlook on how a proof might proceed and how the periodicity may be exploited to describe the infinitely many nilpotent associative FF-algebras of a fixed coclass by a finite set of data.
De Mehmet Haluk Sengun
De Mehmet Haluk Sengun
De Aurel Page
De Alexander Hulpke
De Alexander Hulpke
De Alexander Hulpke
De Paul Gunnells
De Aurel Page
De Peter Patzt
De Peter Patzt
De Peter Patzt
De Jennifer Wilson
De Jennifer Wilson
De Jennifer Wilson
De Haowen Zhang
De Renaud Coulangeon
De Renaud Coulangeon
De Bill Allombert
De Lewis Combes
De Alexander Hulpke
De Alexander Hulpke
De Paul Gunnells
De Paul Gunnells
De Paul Gunnells
De Paul Gunnells
De Graham Ellis
De Graham Ellis
De Graham Ellis
De Graham Ellis
De Graham Ellis
De Philippe Elbaz-Vincent
De Philippe Elbaz-Vincent
De Philippe Elbaz-Vincent
De Bettina Eick
De Petru Constantinescu
De Angelica Babei
De Alexander, D. Rahm
De Benjamin Brück
De Calista Bernard
De Philippe Elbaz-Vincent
De Bettina Eick
De Bettina Eick
De Bettina Eick
De Bettina Eick
De Herbert Gangl
De Zachary Himes
