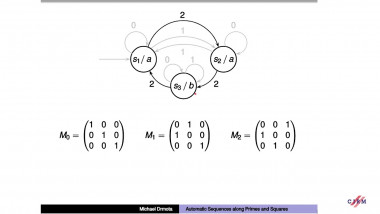
Classification and statistics of cut-and-project sets
De Barak Weiss
Apparaît également dans la collection : Jean-Morlet Chair 2020 - Conference: Diophantine Problems, Determinism and Randomness / Chaire Jean-Morlet 2020 - Conférence : Problèmes diophantiens, déterminisme et aléatoire
We introduce a class of so-called "Ratner-Marklof-Strombergsson measures". These are probability measures supported on cut-and-project sets in Euclidean space of dimension d>1 which are invariant and ergodic for the action of the groups ASL_d(R) or SL_d(R) (affine or linear maps preserving orientation and volume). We classify the measures that can arise in terms of algebraic groups and homogeneous dynamics. Using the classification, we prove analogues of results of Siegel, Weil and Rogers about a Siegel summation formula and identities and bounds involving higher moments. We deduce results about asymptotics, with error estimates, of point-counting and patchcounting for typical cut-and-project sets. Joint work with Rene Ruehr and Yotam Smilansky.