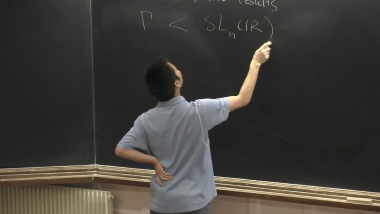There are several interesting ways of ordering groups, but we will focus here on the notion of left-orderability, namely the existence of a total ordering on the group invariant by left translations. In the lectures, we will provide the complete classification of left-orders on irreducible lattices in a semi-simple Lie group of real rank at least 2, based on work of Deroin and Hurtado: such orders exist only if the Lie group has a $\widetilde{SL(2,R)}$-factor and are obtained by pull-back. This answers positively conjectures of Ghys and Witte in the beginning of the 90's. Techniques for the proof include 1) random walks on the group of homeomorphism of the real line, 2) group of almost-periodic homeomorphism of the real line 3) Furstenberg's Poisson formula, 4) dynamics of Cartan subgroups. If time permit, we will discuss the situation in the rank one case.
De Kathryn Mann , David Fisher , Vincent Pecastaing
De Bertrand Deroin
De Bertrand Deroin
De Sebastian Hurtado Salazar
De Bertrand Deroin
De Thang Nguyen
De Thang Nguyen
De Thang Nguyen
De Romain Dujardin
De Romain Dujardin
De Romain Dujardin
De Karin Melnick
De Karin Melnick
De Karin Melnick
De Karin Melnick
De Karin Melnick
De Barbara Schapira
De Barbara Schapira
