
An introduction to state-space models, particle filters, and Sequential Monte Carlo samplers - Part 1
De Nicolas Chopin

An introduction to state-space models, particle filters, and Sequential Monte Carlo samplers - Part 2
De Nicolas Chopin
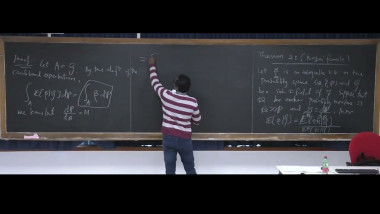
Introduction to Nonlinear Filtering Theory toward Particle Filtering (2/4)
De Fernando Bandhisattambige Pani Wishvamithra
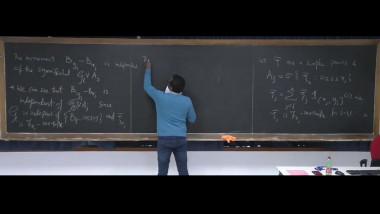
Introduction to Nonlinear Filtering Theory toward Particle Filtering (3/4)
De Fernando Bandhisattambige Pani Wishvamithra

Introduction to Nonlinear Filtering Theory toward Particle Filtering (4/4)
De Fernando Bandhisattambige Pani Wishvamithra











