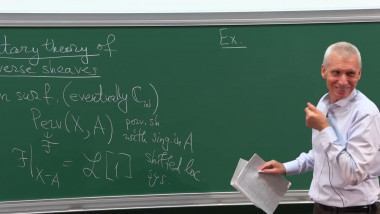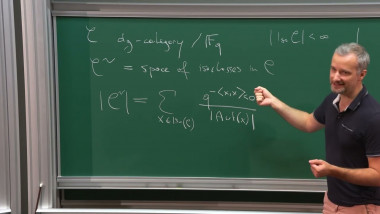Motivic integration was introduced by Maxim Kontsevich in 1995.
About 2007 in the joint work with Maxim, and based on the ideas of motivic integration, we introduced the notion of motivic Donaldson-Thomas invariants of a 3-dimensional Calabi-Yau category endowed with stability condition.
In my talk I will overview how those ideas were used in the joint project with Roman Fedorov and Alexander Soibelman. We computed explicitly motivic Donaldson-Thomas invariants of the moduli stacks of semistable irregular parabolic Higgs bundles and bundles with connection on a smooth projective curve. Here the word irregular parabolic" means that the Higgs field and the connection can have poles of arbitrary order at the fixed points, and theirirregular parts" preserve flags of given types attached to the points.
De Jorgen Ellegaard Andersen
De Alexander Goncharov
De Mina Aganagic
De Yan Soibelman
De Tony Pantev
De Kenji Fukaya
De Denis Auroux
De Davide Gaiotto
De Yuri Tschinkel
De Pavel Etingof
De Alexander Odesskii
De Barbara Schapira
De Barbara Schapira
