Traversing regions of supersolvable hyperplane arrangements and their lattice quotients
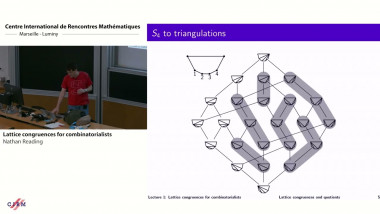
Given an arrangement H of hyperplanes in R^n through the origin, the graph of regions G(H) has a vertex for every region and an edge between any two vertices that correspond to regions separated by exactly one hyperplane. This work focuses on finding a Hamiltonian path or cycle in the graph G(H), i.e., a path or cycle that visits every vertex (=region) exactly once. Our first main result is that if H is a supersolvable arrangement, then the graph of regions G(H) has a Hamiltonian cycle. More generally, we consider quotients of lattice congruences of the poset of regions P(H, R_0), obtained by orienting the graph G(H) away from a particular base region R_0. Our second main result is that if H is supersolvable and R_0 is a canonical base region, then for any lattice congruence ~ on P(H, R_0) =: L, the cover graph of the quotient lattice L/~ has a Hamiltonian path. These paths and cycles are constructed by a generalization of the well-known Steinhaus-Johnson-Trotter algorithm for listing permutations. When applying our two main results to well-known supersolvable arrangements, we recover a number of known Gray code algorithms and also discover several new ones for listing a large variety of combinatorial objects. Our approach also yields new Hamiltonicity results for large classes of polytopes, in particular signed graphic zonotopes and the type B quotientopes of Padrol, Pilaud, and Ritter. In this talk I will highlight the many fascinating connections between geometry, combinatorics, and algorithms arising from these problems on hyperplane arrangements. This talk is based on joint work with Sofia Brenner, Jean Cardinal, Thomas McConville and Arturo Merino