Number of ergodic and generic measures for minimal subshifts
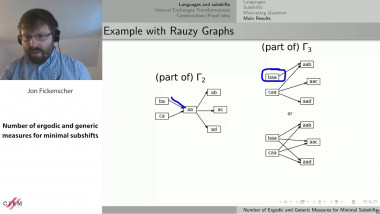
Subshifts on finite alphabets form a class of dynamical systems that bridge topological/ergodic dynamical systems with that of word combinatorics. In 1984, M. Boshernitzan used word combinatorics to provide a bound on the number of ergodic measures for a minimal subshift with bounds on its linear factor complexity growth rate. He further asked if the correct bound for subshifts naturally coded by interval exchange transformations (IETs) could be obtained by word combinatoric methods. (The ”correct” bound is roughly half that obtained by Boshernitzan’s work.) In 2017 and joint with M. Damron, we slightly improved Boshernitzan’s bound by restricting to a smaller class of subshifts that still contained IET subshifts. In recent work, we have further proved the ”correct” bound to subshifts whose languages satisfy a specific word combinatoric condition, which we called the Regular Bispecial Condition. (This condition is equivalent to being Eventually Dendric as independently introduced by F. Dolce and D. Perrin.) During the same time we worked on our 2017 paper, V. Cyr and B. Kra were independently improving Boshernitzan’s results. In 2019, they relaxed the conditions to no longer require minimality and extended Boshernitzan’s bound to generic measures. (Generic measures are those that have generic points, meaning they satisfy the averaging limits as stated in Pointwise Ergodic Theorem. However, there are non-ergodic generic measures.) We have obtained the improved 2017 bound but for generic measures (and on a more general class of subshifts). It should be noted that, to our current knowledge, there does not exist a proof of the correct bound of generic measures for minimal IETs (by any method).In this talk, I will discuss these recent results and highlight related open problems.