Additive combinatorics in Marseille / Combinatoire additive à Marseille

Collection Additive combinatorics in Marseille / Combinatoire additive à Marseille

Organisateur(s) Hennecart, François ; Plagne, Alain ; Szemerédi, Endre

Date(s) 07/09/2015 - 11/09/2015

URL associée http://conferences.cirm-math.fr/1107.html

00:00:00 / 00:00:00

4 7

On sum sets of sets having small product set

De Sergei V. Konyagin

Apparaît également dans la collection : Exposés de recherche

We improve a result of Solymosi on sum-products in $\mathbb{R}$, namely, we prove that max $(|A+A|,|AA|\gg |A|^{4/3+c}$, where $c>0$ is an absolute constant. New lower bounds for sums of sets with small product set are found. Previous results are improved effectively for sets $A\subset \mathbb{R}$ with $|AA| \le |A|^{4/3}$. Joint work with I. D. Schkredov.

Informations sur la vidéo

Date de captation 10/09/2015
Date de publication 06/10/2015
Institut CIRM
Licence CC BY NC ND
Langue Anglais
Audience Chercheurs
Réalisateur(s) Guillaume Hennenfent
Format MP4

Données de citation

DOI 10.24350/CIRM.V.18830303
Citer cette vidéo Konyagin, Sergei V. (10/09/2015). On sum sets of sets having small product set. CIRM. Audiovisual resource. DOI: 10.24350/CIRM.V.18830303
URL https://dx.doi.org/10.24350/CIRM.V.18830303

Domaine(s)

Bibliographie

Konyagin, S., & Shkredov, I.D. (2015). On sum sets of sets, having small product set. <arXiv:1503.05771> - http://arxiv.org/abs/1503.05771

Codes MSC

Dernières questions liées sur MathOverflow

Pour poser une question, votre compte Carmin.tv doit être connecté à mathoverflow

Poser une question sur MathOverflow

Toutes les vidéos de la collection

25:23

publiée le 6 octobre 2015

A characterization of class groups via sets of lengths

De Alfred Geroldinger

33:56

publiée le 30 septembre 2015

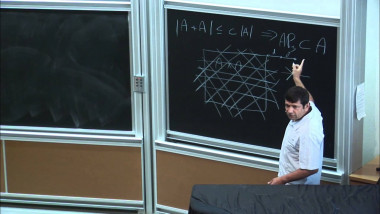
Incidences in Cartesian products

De Jozsef Solymosi

25:23

publiée le 29 septembre 2015

Interview at CIRM: Endre Szemerédi

De Endre Szemerédi

23:56

publiée le 6 octobre 2015

On sum sets of sets having small product set

De Sergei V. Konyagin

36:25

publiée le 6 octobre 2015

Maximum size of a set of integers with no two adding up to a square

De Endre Szemerédi

35:00

publiée le 6 octobre 2015

$k$-sum free sets in $[0,1]$

De Anne de Roton

33:07

publiée le 6 octobre 2015

Structure theory of set addition, a review

De Gregory A. Freiman

Copyright Carmin.tv 2025

Donner son avis