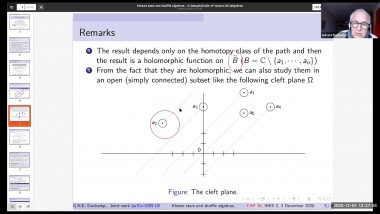
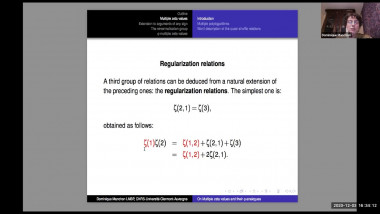
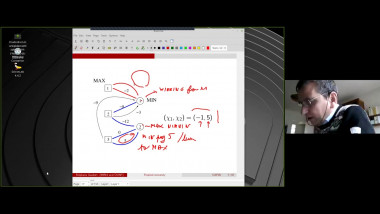
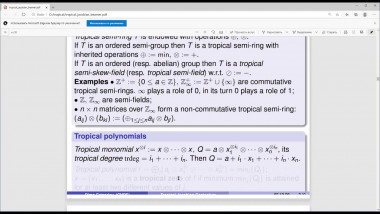
Quotients of Symmetric Polynomial Rings Deforming the Cohomology of the Grassmannian
One of the many connections between Grassmannians and combinatorics is cohomological: The cohomology ring of a Grassmannian $Gr(k,n)$ is a quotient of the ring $S$ of symmetric polynomials in k variables. More precisely, it is the quotient of $S$ by the ideal generated by the $k$ consecutive complete homogeneous symmetric polynomials $h_{n−k},h_{n−k+1},…,h_n$. We deform this quotient, by replacing the ideal by the ideal generated by $h_{n−k}−a_1,h_{n−k+1}−a_2,…,h_n−a_k$ for some $k$ fixed elements $a_1,a_2,…,a_k$ of the base ring. This generalizes both the classical and the quantum cohomology rings of $Gr(k,n)$. We find three bases for the new quotient, as well as an $S_3$-symmetry of its structure constants, a “rim hook rule” for straightening arbitrary Schur polynomials, and a fairly complicated Pieri rule. We conjecture that the structure constants are nonnegative in an appropriate sense (treating the $a_i$ as signed indeterminate), which suggests a geometric or combinatorial meaning for the quotient.